Patrz pod nogi! Parkiety powtarzalne i te niepowtarzalne
Czeka mnie cyklinowanie parkietu. Z matematycznego punktu widzenia mój parkiet to nic nadzwyczajnego - ot, zwykła jodełka - wzór złożony z samych prostokątów. Ale bywają i parkiety niepowtarzalne - aperiodyczne. Warto się im bliżej przyjrzeć.
Plaster miodu, kostka Bauma, szachownica czy pepitka... Czy nam się to podoba, czy nie, parkiety towarzyszą nam na każdym kroku. Plączą się pod nogami w różnych przejściach, przykuwają wzrok w toaletach, zwracają uwagę na tkaninach...
Parkietaż rządzi się dość prostymi zasadami. Chodzi o to, żeby używając niewielu rodzajów obiektów o takim samym kształcie (płytek) wypełnić szczelnie całą powierzchnię. Czasem również nieskończenie wielką. A gdzie mowa o nieskończonościach, tam prędzej czy później pojawią się matematycy.

Jeden z parkietów M. C. Eschera. Fot: mararie, Flickr
Pokazują oni np. że jedynie wśród wielokątów foremnych (figury, których wszystkie kąty takie same, a boki - równe) nie ma zbyt wielkiego wyboru płytek do parkietów. Płaszczyznę można - nie pozostawiając dziur - wypełnić jedynie trójkątami równobocznymi (zygzak), albo kwadratami (szachownica), albo sześciokątami (plaster miodu). Pozostałe wielokąty foremne nie zdają tu egzaminu. Dodatkowo istnieją parkiety, w których płytkami jest kilka różnych wielokątów foremnych, a w każdym wierzchołku układ wielokątów jest jednakowy. To tzw. parkietaże archimedesowskie. (W "Niezwykłych liczbach Iana Stewarta" Ian Stewart pisze, że takich parkietaży archimedesowskich jest dziewięć, ale mam wrażenie, że mój ulubiony popularyzator matematyki tu się pomylił. Ile jest takich parkietów? Pomóżcie!)
Płytki parkietu mogą mieć i bardziej wymyślne kształty. Mistrzem oryginalnych parkietów był artysta M. C. Escher. W dzieciństwie godzinami wpatrywałam się w jego grafiki, na których dziury między aniołami szczelnie wypełnione były przez diabły (a może na odwrót), ryby przeplatały się z ptakami, a przestrzeń uzupełniali rycerze lub jaszczurki. Było to fascynujące, choć dopiero z czasem uświadomiłam sobie, że grafiki te są pomysłami właśnie na parkiety.

Jeden z parkietów M. C. Eschera. Źródło: https://en.wikipedia.org/
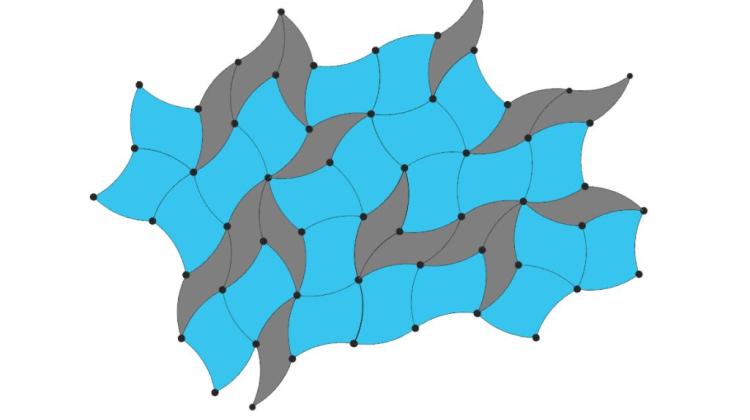
Ostatnio przypomniałam sobie o sztuce oraz nauce parkietażu podczas wakacji - w Sztokholmie na stacji kolejowej Stockholm Södra. Wypatrzyłam tam parkiet, dość niestandardowy. Składa się jedynie z dwóch rodzajów płytek oraz ich odbić lustrzanych (czyli w sumie 4 rodzaje kształtów). Choć figury są tylko cztery, w układzie płytek nie widać żadnej regularności. Ich wzór - na pierwszy rzut oka - nigdy się nie powtarza. Czyżby to był parkietaż nieperiodyczny?

Posadzka – czyżby parkietaż nieperiodyczny? - na stacji Stockholm Södra. Fot.: Tomasz Gancarczyk
Parkiety aperiodyczne to dla matematyków niezła gratka - w porównaniu z poczciwą szachownicą są naprawdę chaotyczne. Choć w takim parkiecie płytek bywa tylko kilka rodzajów, to kiedy zapełni się nimi powierzchnię, nie będą one tworzyć żadnego powtarzalnego wzoru. Nigdy. Chodzi o to, że nie da się znaleźć takiego fragmentu układu, który można byłoby przesuwać (skopiować i wklejać w innym miejscu - bez obracania) tak, by pokryć całą przestrzeń. W parkietach aperiodycznych po prostu nie ma powtarzalności.
Kilka wzorów parkietów aperiodycznych pokazał Roger Penrose - brytyjski fizyk i matematyk - w latach 70. ub. wieku. Zaproponował m.in. parkiet aperiodyczny składający się jedynie z dwóch rodzajów rombów - jeden - "chudy" o kątach po 36 i 144 stopni i drugi - "grubszy" o kątach po 72 i 108 stopni.

Parkietaż Perose’a. Ilustracja: Inductiveload https://commons.wikimedia.org/w/index.php?curid=5839079
I coś mi się wydaje, że parkiet w Sztokholmie to twórcza interpretacja tego właśnie parkietu Penrose\'a. Boki rombów są jednak pofalowane, przez co romby przestały być symetryczne. Aby zapełnić parkiet, potrzebne były zwierciadlane odbicia tych figur. Z takim jedynie zestawem figur nie można na peronie (ani nigdzie indziej) ułożyć powtarzającego się co stały okres wzoru. Układ płytek nie miał szansy się powtórzyć, nawet gdyby peron był nieskończenie długi. Czyż nie jest to pociągająca myśl?
Nauka w Polsce, Ludwika Tomala
Przed dodaniem komentarza prosimy o zapoznanie z Regulaminem forum serwisu Nauka w Polsce.

















