
Poprawa dokładności sondaży przedwyborczych i prognoz ekonomicznych, projektowanie nowych wytrzymałych materiałów, dokładniejsze wyznaczanie ryzyka osteoporozy czy chorób neurologicznych - w rozwiązywaniu tych oraz wielu innych, praktycznych problemów pomóc może matematyka - mówi dr Paweł Dłotko.
Socjolodzy, ekonomiści, lekarze, inżynierowie często próbują rozwiązywać problemy ze swoich dziedzin zaczynając od podstaw. Tymczasem nierzadko zamiast odkrywać na nowo koło, można zastosować gotowe - i o wiele bardziej zaawansowane - narzędzia dostępne od dawna w matematyce. Trzeba tylko wiedzieć, jak tych narzędzi użyć w nowych rozwiązaniach.
I tu na pomoc przedstawicielom innych nauk przychodzić chce z pomocą warszawskie centrum Dioscuri Topologicznej Analizy Danych przy Instytucie Matematycznym PAN. "Staramy się używać metod znanych z matematyki poza matematyką, a więc robimy coś, co można określić mianem matematyki stosowanej" - mówi w rozmowie z PAP szef centrum Dioscuri dr Paweł Dłotko. Badacz chce, by centrum Dioscuri było przestrzenią, gdzie matematycy rozmawiają z przedstawicielami innych dziedzin nauki i wspólnie wypracowują potrzebne tam narzędzia matematyczne.
Przykład symulacji prądu w skomplikowanym (zawęźlony przewodniku), credit: Ruben Specogna
"Matematyka nazywana jest królową nauk nie dlatego, że jest skomplikowana czy koncepcyjnie trudna, ale dlatego, że jest wszechobecnie pożyteczna" - komentuje naukowiec.
Zaznacza, że praktyczne zastosowania matematyki często były dotąd ograniczone do takich obszarów jak równania różniczkowe. Tak było choćby od czasów Newtona, który opisywał za ich pomocą grawitację. "A my robimy coś innego - do rozwiązywania problemów używamy metod z tzw. topologii" - mówi dr Dłotko.
Topologia to obszar matematyki, który - w dużym uproszczeniu - opisuje kształty obiektów czy danych i zajmuje się ich ciągłymi przekształceniami. "Po kształcie, sylwetce można odróżnić od siebie np. różne rasy psów. Jednak sformalizowanie, czym jest ten kształt danej rasy psa, jest mniej trywialne. A to przecież obrazy 2-wymiarowe. Tymczasem my w topologii musimy się mierzyć z danymi o bardzo dużej liczbie wymiarów co dodatkowo zwiększa poziom trudności" - tłumaczy naukowiec.
Dr Dłotko opowiada, że w ramach swoich wcześniejszych badań pokazywał już, że topologia może znaleźć zastosowanie w naukach społecznych - np. w dokładniejszym prognozowaniu wyników wyborów. "Brytyjczycy w 2016 r. zagłosowali za wyjściem z Unii Europejskiej, mimo że sondaże wskazywały, że do brexitu nie dojdzie. Według mnie to była porażka modelowania matematycznego" - mówi. Dodaje, że wraz z brytyjskimi politologami i socjologami przeanalizował wtedy dane ze spisu powszechnego i badacze wybrali stamtąd zbiór odpowiedzi, które mogły mieć związek z poglądami dotyczącymi brexitu. "Zwizualizowaliśmy te dane za pomocą narzędzi topologicznych i udało się nam zobaczyć pewne nowe zależności. Choćby to, że ludzie, którzy wspierali brexit, byli grupą zdecydowanie bardziej jednorodną niż osoby przeciwne wyjściu Wielkiej Brytanii z UE. A jeśli to grupa jednorodna - ludzie o podobnych zainteresowaniach, oglądający te same programy - to łatwiej ich zmobilizować. Trudniej zaś zmobilizować grupę różnorodną – w tym przypadku przeciwników brexitu" - komentuje matematyk. Dodaje, że jego koledzy politolodzy kompletują teraz podobne dane dotyczące wyborów w USA.
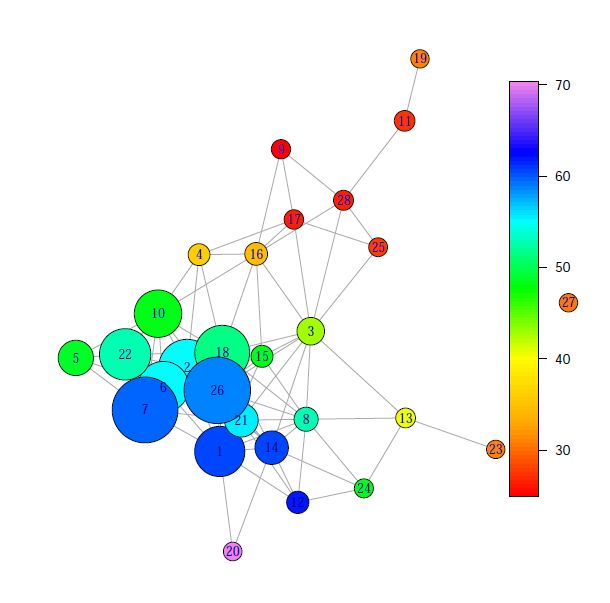
Rys: wizualizacja danych ze spisu powszechnego w UK, na którym zaznaczono kolorami wsparcie brexitu. Źródło: https://arxiv.org/abs/1909.03490 https://ukandeu.ac.uk/constituency-voting-patterns-illustrate-a-close-election-ahead/
Innym z obszarów, w których wykorzystać można topologię, jest ekonomia. Matematyk opowiada, że w jednym ze swoich badań analizował funkcję używaną przez amerykańskie banki jako wstępne kryterium, czy danej firmie przyznać pożyczkę. Wskaźnik ten, bazujący na regresji logistycznej wykorzystującej kilka do kilkunastu parametrów charakteryzujących kondycję danej firmy, pomaga bankom ustalić ryzyko rychłego jej bankructwa. Nie jest to jednak wskaźnik perfekcyjny. Z historycznych danych wiadomo, że sporo firm z niską wartością wskaźnika radziło sobie nieźle, zaś te, które faktycznie zbankrutowały, można było scharakteryzować pewnym specyficznym układem parametrów w obrębie firm posiadających słabą kondycję. Dokładne zrozumienie kształtu i pozycji tego wielowymiarowego układu parametrów charakterystycznych dla bankrutujących firm jest tematem obecnych prac badawczych. „Mamy nadzieję, że pozwoli nam to zbudować lepsze, bazujące na danych i ich kształcie, kryteria oceny kondycji firm przedsiębiorstw” – komentuje matematyk.
Jeden z obecnych projektów w ramach centrum Dioscuri dotyczy tego, by dzięki metodom matematycznym sklasyfikować różne typy neuronów - komórek nerwowych pracujących choćby w mózgu. "O ile neurolodzy są w stanie wydobyć z mózgu pojedyncze neurony, to żeby stwierdzić, jaki to typ neuronu i jaka jest jego funkcja w mózgu, należy poprosić o opinię eksperta. A my chcemy zautomatyzować ten proces, sprawić, żeby klasyfikacja typów neuronów nie była związana z czyjąś opinią, ale żeby była czymś dobrze zdefiniowanym" – tłumaczy rozmówca PAP. Dlatego naukowcy starają się stworzyć kolekcję obiektów matematycznych, które opisują kształt neuronów. Dr Dłotko porównuje neuron do drzewa. "Opisujemy więc, jak bardzo drzewo się rozgałęzia, jak bardzo jego gałęzie się wiją, jak może przepływać przez nie prąd. Teraz mamy kolekcję około 10 takich niezmienników, dzięki czemu jesteśmy w stanie efektywnie prowadzić klasyfikację neuronów" - mówi. I opisuje, że w ramach badań naukowcy zastanawiają się np. czy pewne choroby neurologiczne mogą mieć związek z kształtem neuronów.
Opis procedury klasyfikacji neuronu, z pracy https://www.biorxiv.org/content/10.1101/2021.01.15.426800v1.abstract
Kolejny temat, w który zaangażowali się topolodzy z Warszawy, to klasyfikacja struktury kości beleczkowych. "Wspólnie z lekarzami i radiologami patrzymy na problemy związane z diagnostyką osteoporozy" - mówi. Tłumaczy, że obecnie diagnoza bazuje na badaniu gęstości kości. Jeśli czyjaś gęstość kości jest poniżej pewnych wartości średnich – proponowana jest terapia. "Podobno jest jednak spora grupa pacjentów, którzy - choć są w normie, to mają charakterystyczne dla osteoporozy złamania. I są pacjenci poniżej normy, u których przez wiele lat do żadnych złamań nie dochodzi. Nasza hipoteza jest taka, że znaczenie ma nie tylko gęstość kości, ale i struktura kości beleczkowej. Strukturę tę należy jednak umieć obiektywnie opisać w oparciu o dostępne obrazy medyczne. Dlatego my patrząc na strukturę kości staramy się policzyć ilość dziur, ich wielkość, grubość beleczek i skorelować to z odpornością kości" - mówi matematyk.
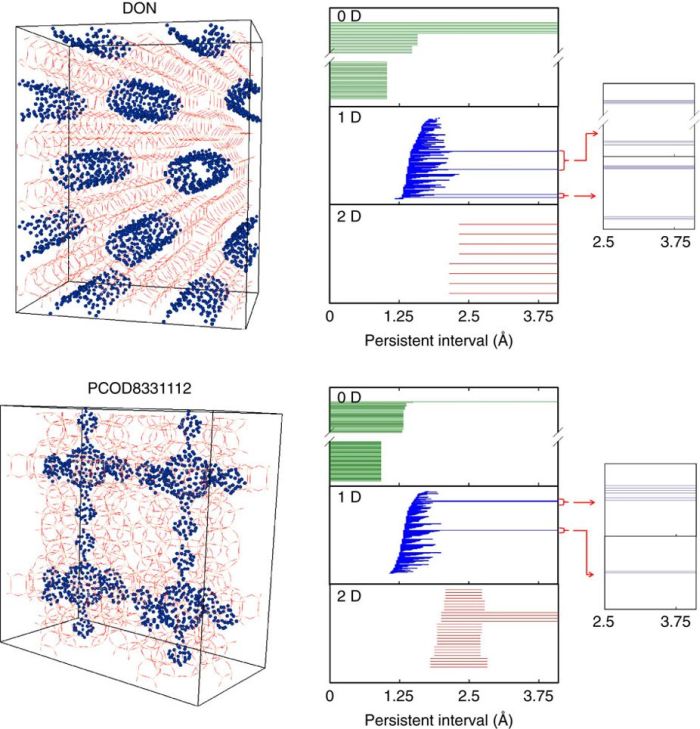
Uzyskiwanie topologicznych niezmienników na podstawie punktów próbkowanych z porów. Źródło: Y. Lee et al., Nature Communications 2017https://www.nature.com/articles/ncomms15396
Badania z zakresu topologii przydać się też mogą w poszukaniu materiałów o optymalnych właściwościach. Wśród nich są np. zeolity, nanoporowate struktury metaloorganiczne, stosowane np. w proszkach do prania. Budowa zeolitów może się bardzo różnić: są dostępne bazy milionów możliwości przestrzennego ułożenia ich podstawowych cegiełek dające różne materiały. Wyzwanie polega na tym, żeby wśród nich wyszukać te, które najlepiej będą spełniać z góry zadane wymagania: np. magazynować metan czy filtrować dwutlenek węgla. Odpowiednie scharakteryzowanie tych obiektów za pomocą metod topologicznych, sprawi, że przeszukiwanie baz zeolitów stanie się o wiele prostszym zadaniem. Badania na ten temat ukazały się w Nature Communications https://www.nature.com/articles/ncomms15396
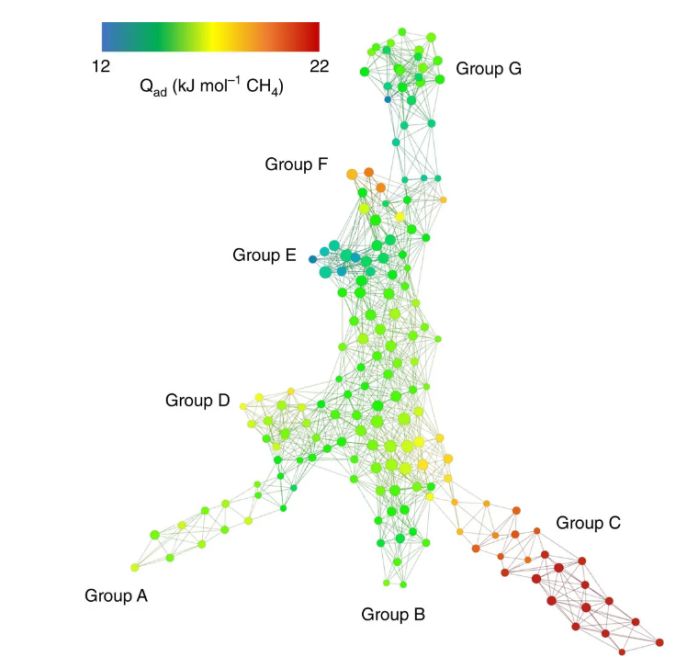
Rodzaje materiałów nanoporowatych, Źródło: Y. Lee et al., Nature Communications 2017, https://www.nature.com/articles/ncomms15396
"W tych wszystkich projektach matematyka nie jest wiodącą dyscypliną, ale jest przybornikiem, który daje narzędzia do rozwiązania różnych problemów" - mówi dr Dłotko. I zaznacza, że warunkiem koniecznym badań jest zawsze współpraca interdyscyplinarna.

Rys: Wizualizacja przestrzeni wielomianów Jonsea dla węzłów do 15 przecięć pokolorowana przez knot signature.
"Przedstawiciele innych dziedzin: medycyny, neurologii, inżynierii - muszą chcieć z nami rozmawiać, a to wcale nie jest trywialne. To wymaga znalezienia wspólnego języka" - mówi.
Dodaje, że największym wyzwaniem w działaniu centrum Dioscuri są ludzie - badacze, którzy mają pojęcie zarówno o matematyce, jak i o programowaniu. "A to jest problem, bo jeśli ktoś ma smykałkę do tych obu obszarów, to jest łakomym kąskiem dla firm. A choć mogę zaoferować współpracownikom stypendium na europejskim poziomie, to jeśli chodzi o zarobki, nie jestem w stanie konkurować z dużymi firmami, które te poszukują ludzi o podobnym profilu" - kończy dr Dłotko i zachęca matematyków, którzy umieją programować, do współpracy z centrum Dioscuri.
PAP - Nauka w Polsce, Ludwika Tomala
lt/ ekr/


