Matematyk o tym, że również rozsupływanie węzłów gordyjskich ma sens

Do rozwiązania jednego problemu prowadzić może wiele dróg. Niektóre z nich zwodzą na manowce. Czasem jednak etap zabrnięcia w "bagno" przydaje się w prowadzeniu badań. Dr hab. Maciej Borodzik, matematyk zajmujący się teorią węzłów, opowiada o rozwiązywaniu problemów, które wydają się nie do rozwiązania.
Matematyk dr hab. Maciej Borodzik z Uniwersytetu Warszawskiego zajmuje się w swoich badaniach teorią węzłów. W ramach tej teorii naukowcy badają własności węzłów - wyobrażonych tworów zawiązanych na rozciągliwych cienkich sznurkach ze sklejonymi końcami.
Niektóre węzły daje się rozwiązać, inne - przekształcić do postaci, którą lepiej znamy. A innych - o ile nie stosujemy cięć lub oszustw - po prostu rozwiązać się nie da. Podobnie jest z problemami, które napotykamy w życiu.
NIE KAŻDY WĘZEŁ JEST GORDYJSKI

Fot.: Nie zawsze problem, który wydaje się nie do rozwiązania jest taki skomplikowany. Fot. Kuchtact / CC BY-SA
Czasem problemy, których nie da się rozwiązać, można pomylić z tymi bardzo trudnymi. "Bywa tak, że człowiek siada nad pustą kartką i nie napisze nic przez miesiąc. Albo i rok. Nie widzi drogi. To zwykle przypada na czas robienia doktoratu. Wiele osób wtedy rezygnuje. Ale ten etap 'bagna' jest konieczny, żeby - przynajmniej w matematyce - prowadzić dobre badania. Człowiek się wtedy rozwija i zaczyna dostrzegać dalszą drogę" - opisuje dr Borodzik.
ŚLEPE ULICZKI UCZĄ NAS WIDZIEĆ
"W matematyce jest mnóstwo sposobów podejścia do rozwiązania danego tematu, ale niektóre z nich zwodzą na manowce" - mówi. Według niego jednak nawet, jeśli nie uda się rozwiązać problemu, to czas spędzony na błądzeniu nie musi być czasem straconym - człowiek się wtedy dużo uczy.
"Poznaje się wtedy i testuje sposoby myślenia czy narzędzia, które mogą się przydać na kolejnych etapach pracy. Więc nawet, jeśli te chybione pomysły nie przydadzą się w dążeniu do jednego celu, to może przydadzą się w osiąganiu kolejnych" - mówi.
A to znaczy, że nawet cierpliwe rozwiązywanie węzła gordyjskiego może mieć większy sens niż jego przecięcie.
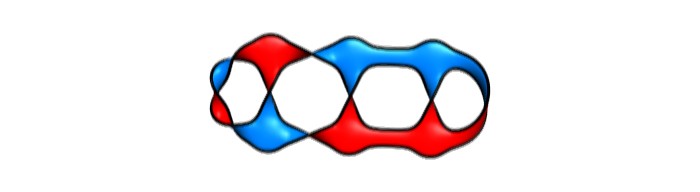
Fot: Powierzchnie Seiferta rozpięte na sznurze z węzłem. Ilustracja wykonana przy użyciu darmowego programu SeifertView
WĘZŁY BARDZO CHŁONNE
Kiedy rozwiązuje się problem, może się okazać, że właściwych dróg do osiągnięcia jednego celu może być sporo. "A akurat w węzłach jest wszystko - można tam używać technik z bardzo szerokiego spektrum matematyki" - mówi naukowiec.
Jak opowiada, on sam wywodzi się z obszaru matematyki, który nazywa się teorią osobliwości ("chodzi tam o przestrzenie, które mają 'dzióbki'" - tłumaczy). A dogłębna wiedza w tej "osobliwej" jak na badanie teorii węzłów dziedzinie, daje mu w niektórych miejscach przewagę nad badaczami, którzy nie mają tego zaplecza.
ARANŻUJMY SPLOTY OKOLICZNOŚCI
Dr Borodzik opowiada, że o pracy badawczej warto rozmawiać z ludźmi mającymi nieco inne spojrzenie. Mogą oni dysponować mniej oczywistymi, ale bardzo przydatnymi narzędziami.
Naukowiec wspomina, jak kiedyś utknął z jakimś problemem na długie tygodnie, aż zagadnął o to kogoś na konferencji naukowej. Ta osoba akurat znała metody i wystarczyło jej parę minut, żeby pokazać rozwiązanie. "Nawet rozmowy o głupotach czasami się konkretyzują - czasem wychodzi z nich duży projekt, a czasem - w szybka praca" - opowiada.
Fot: Przykładowe węzły. Rys: kolaż z rysunkami AnonMoos, domena publiczna
KRÓTKO I WĘZŁOWATO O TYM, PO CO BADAĆ WĘZŁY
Kiedy matematyk rozwiązuje jakiś problem, przed oczami czasem ma jego piękno. Ale warto, by z tyłu głowy miał szerszy kontekst swoich badań.
"Węzły w matematyce mają fundamentalne zastosowanie przy rozumieniu geometrii 3- i 4-wymiarowej" - mówi matematyk. Opowiada, że jeśli węzeł wytnie się z przestrzeni, a potem wklei go inaczej, otrzymuje się zakrzywioną przestrzeń. "Wszystkie zakrzywione w trzech wymiarach przestrzenie mogę otrzymać za pomocą takiej operacji - lub ich serii" - mówi naukowiec.
W takich przestrzeniach zakrzywionych dziać się mogą - jak na nasze standardy - bardzo dziwne rzeczy. Może się więc np. okazać, że jeśli dwie osoby będą szły w tym samym kierunku po tej samej linii prostej, to przejdą zupełnie inne trasy i trafią w to samo miejsce pod innymi kątami. Takie zakrzywione przestrzenie mogą istnieć gdzieś we Wszechświecie, np. w pobliżu czarnych dziur. Dzięki teorii węzłów będzie już metoda, by je opisywać.

Fot: Powierzchnie Seiferta to powierzchnie, których granicami jest węzeł. Fot: uzyskane dzięki darmowemu programowi SeifertView
NIEOCZEKIWANE WIĄZANIE KOŃCA Z KOŃCEM
Czasami, kiedy w czasie badań zaczyna się przypadkiem pociągać za wystające sznurki - okazuje się, że prowadzą one do ciekawych węzełków, którym warto się przyjrzeć.
Dr Borodzik śmieje się, że miał kiedyś z kolegą pomysł, aby udowodnić, że jeśli hipoteza Riemanna jest prawdziwa, to pewnego węzła nie da się rozwiązać w dwóch "ruchach" (ruch to w tym przypadku przeskoczeniu jednego fragmentu sznurka przez drugi). Hipoteza Riemanna dotyczy obszaru matematyki zwanego teorią liczb. Dla matematyków powiązanie teorii liczb i teorii węzłów może się wydawać niedorzecznym pomysłem - zdają się one nie mieć ze sobą nic wspólnego. "Mimo że byłby to więc sensowny wynik, to zastanawialiśmy się, czy nie opublikować tych badań 1 kwietnia, w Prima Aprilis, bo to był tak dziwny pomysł" - śmieje się naukowiec.
GŁODNI WIEDZY I ZŁAKNIENI PRECLI
Rozwiązywanie skomplikowanych problemów matematycznych nie byłoby tak pociągające, gdyby nie to uczucie, kiedy wpada się na pomysł i zaczyna widzieć drogę do celu.
"Czasem jak już złapię trop, to zajmuję się tylko jedną rzeczą. Inne tematy odsuwam na bok, zawalam terminy na sprawy papierkowe. Czuję, że tak po prostu trzeba" - opisuje dr Borodzik.
"To uczucie podobne jest do emocji, które towarzyszą czytaniu kryminału, wciągającej książki. Tylko, że jest ono o wiele intensywniejsze" - opowiada. I dodaje, że czasem, kiedy wstaje rano i zastanawia się, którym projektem się dziś zajmie, czuje się trochę jak żarłok, który zagląda do lodówki. "To uzależniające. Jest w tym forma łakomstwa!" - mówi.
SPOJRZENIE Z SUPEŁ-POZYCJI
Aby dać przedsmak tego, co u matematyków wywołuje w teorii węzłów takie emocje, naukowiec opowiada, że węzły najtrudniej rozwiązywać w przestrzeniach 3- i 4-wymiarowych. A już w przestrzeniach, gdzie wymiarów jest co najmniej 5, dochodzi do głosu pewien matematyczny trik (trik Whitneya), który sprawia, że wszelkie zakrzywienia przestrzeni można opisać za pomocą operacji algebraicznych. "W przestrzeni o pięciu i więcej wymiarach trik ten działa. A w 3- i 4- wymiarowej nie ma na niego miejsca" - mówi. Rzeczywistość, którą zwykliśmy postrzegać naszymi zmysłami, jest więc o wiele bardziej "poplątana", niż gdybyśmy wymiarów postrzegali więcej.
Dra Borodzika w jego badaniach pociąga zwłaszcza zagadnienie węzła narysowanego na 3-wymiarowej sferze. "Zastanawiam się m.in., jaką powierzchnię ogranicza on w czterech wymiarach" - streszcza. I dodaje, że matematycy od kilkudziesięciu lat nie znaleźli jeszcze rozwiązania tego problemu. A paradoksalnie pytania dotyczące dość prostych obiektów - takich jak sfery - są trudniejsze. "To obiekty tak gładkie, że nie ma się o co zaczepić" - uśmiecha się badacz.
Powyżej: Przykładowe węzły. Rys. kolaż z użyciem grafik AnonMoos, domena publiczna
NIE PRZYWIĄZUJ SIĘ DO WSZYSTKICH SWOICH POMYSŁÓW
Naukowiec tłumaczy, że pomysły, na które się wpada, nie zawsze okazują się słuszne. Więc nie zawsze warto się do nich przywiązywać. "Najpierw piszę pracę. I piszę ją błędnie. A potem poprawiam. Między pierwszą wersją pracy a wersją ostatnią jest tyle zmian, że przeżywają niekiedy tylko niektóre kropki i przecinki. To jednak nie znaczy, że pierwsza wersja pracy nie jest potrzebna. Jest! Bo bez niej nie byłoby wersji następnej!" - zwraca uwagę.
NA SPLOCIE DZIEDZIN
"Matematyka zajmuje się zagadnieniami, które interesują tylko matematyków. Ale raz na jakiś czas ktoś odkrywa, że dany obszar jest potrzebny do rozwiązywania innych problemów" - mówi.

Fot: Powierzchnie Seiferta to powierzchnie, których granicami jest węzeł. Fot: uzyskane dzięki darmowemu programowi SeifertView
Podaje przykład, że w przyrodzie węzły mogą się pojawiać np. w łańcuchu DNA. A jeśli się pojawią - może być problem z produkcją jakiegoś białka. Rozmówca PAP opowiada, że pomagał biologom rozwiązywać problemy w tym zakresie.
Badacz przyznaje jednak, że praca na styku dwóch dziedzin była dla niego trudna. Opowiada, że naukowcy z rożnych obszarów nauki wykorzystują inne sposoby myślenia, upatrują w swojej pracy innych przyjemności i inaczej opowiadają o swoich badaniach - np. w publikacjach naukowych. Patrząc więc na ten sam węzeł widzą zupełnie co innego. A to problem dotyczący rozwoju badań interdyscyplinarnych, który również - na razie wydaje się węzłem gordyjskim.
PAP - Nauka w Polsce, Ludwika Tomala
lt/ zan/
Przed dodaniem komentarza prosimy o zapoznanie z Regulaminem forum serwisu Nauka w Polsce.